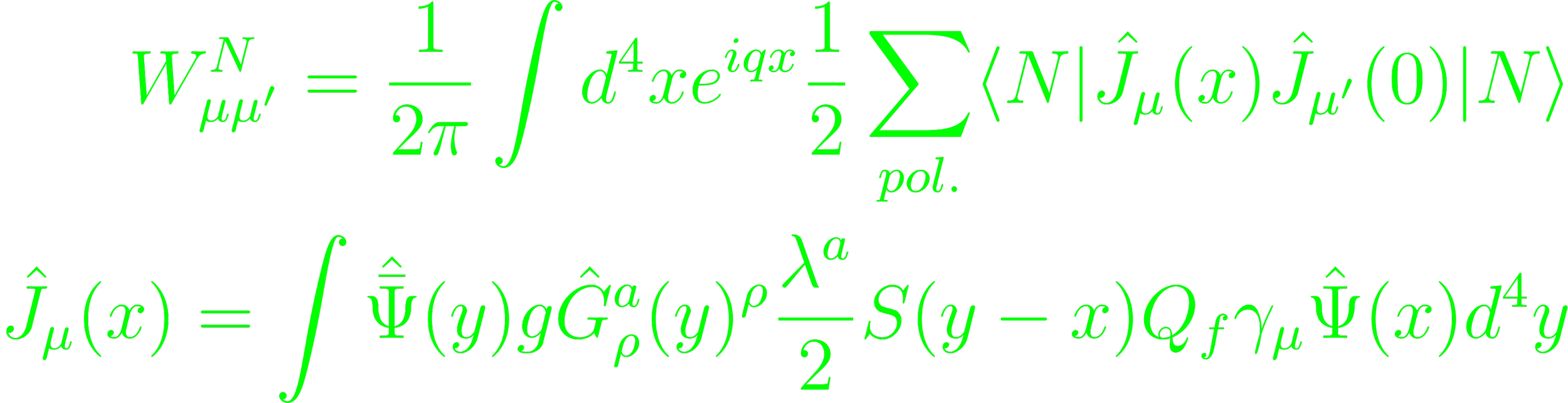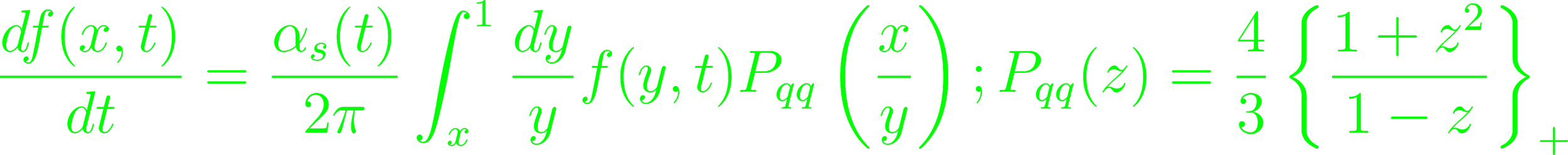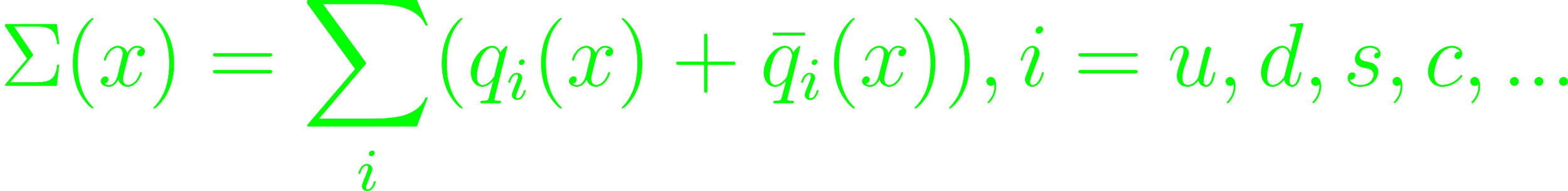Quantum Chromodynamics 2026, 05 - GLAP Equations

The Gribov-Lipatov-Altarelli-Parisi (GLAP) equations give perturbative QCD corrections on distributions for partons in deep inelastic scattering processes (p. 239). The scattering parton and emitted gluon are treated as free particles. The resulting diagrams are similar to Compton scattering diagrams. Their contribution to the scattering tensor can be evaluated in analogy to the QED graphs. The scattering amplitude is

The space-time coordinate x characterizes the point of interaction between photon and photon-current. The quarks inside the nucleon are treated as free particles, so the product of the current operators in hadronic state is foregone in favour of free quark states, and tensor W_μν can be calculated perturbatively. The current action implies that the operators Ψ can be replaced by the quark wave functions (p. 240). The quark and gluon wave functions can be taken as plane waves (p.241). The propagators have to be substituted by δ-functions for particles in the inner lines of the graphs (Eq. 5.6). In applying the Breit system, the kinematics of the process are cylindrically symmetric, which simplifies the integrals (Eq. 5.15). This geometry makes solving the integral for K_μ easier. The Θ-function eventually leads to a divergent integral, which is cut off at -λ² (Eq. 5.35). Any such approach will only yield solutions for a small number of graphs. Given a value for the structure functions, the energy spectrum of these graphs can be correlated (Fig. 5.6). For increasing momentum transfers QCD becomes more important, and more (anti-)quarks and gluons occur. The total momentum of the nucleon is distributed over more partons, so the distribution function has to decrease for large momentum fractions (Eq. 5.51). Gluons contribute to the sum of the partition function, but not to the structure functions (p. 257). The expression for the partition function as an integral of another partition function constitutes the GLAP equation.

(Eq. 5.54, 5.58). The quark fine-structure can be resolved by the exchanged photon given sufficient photon momentum. P_qq can be used as a splitting function. Write single quark distribution functions as a total quark distribution