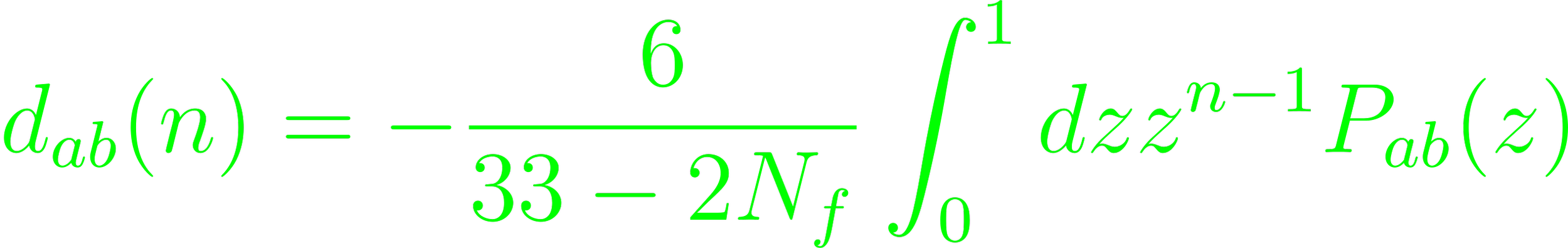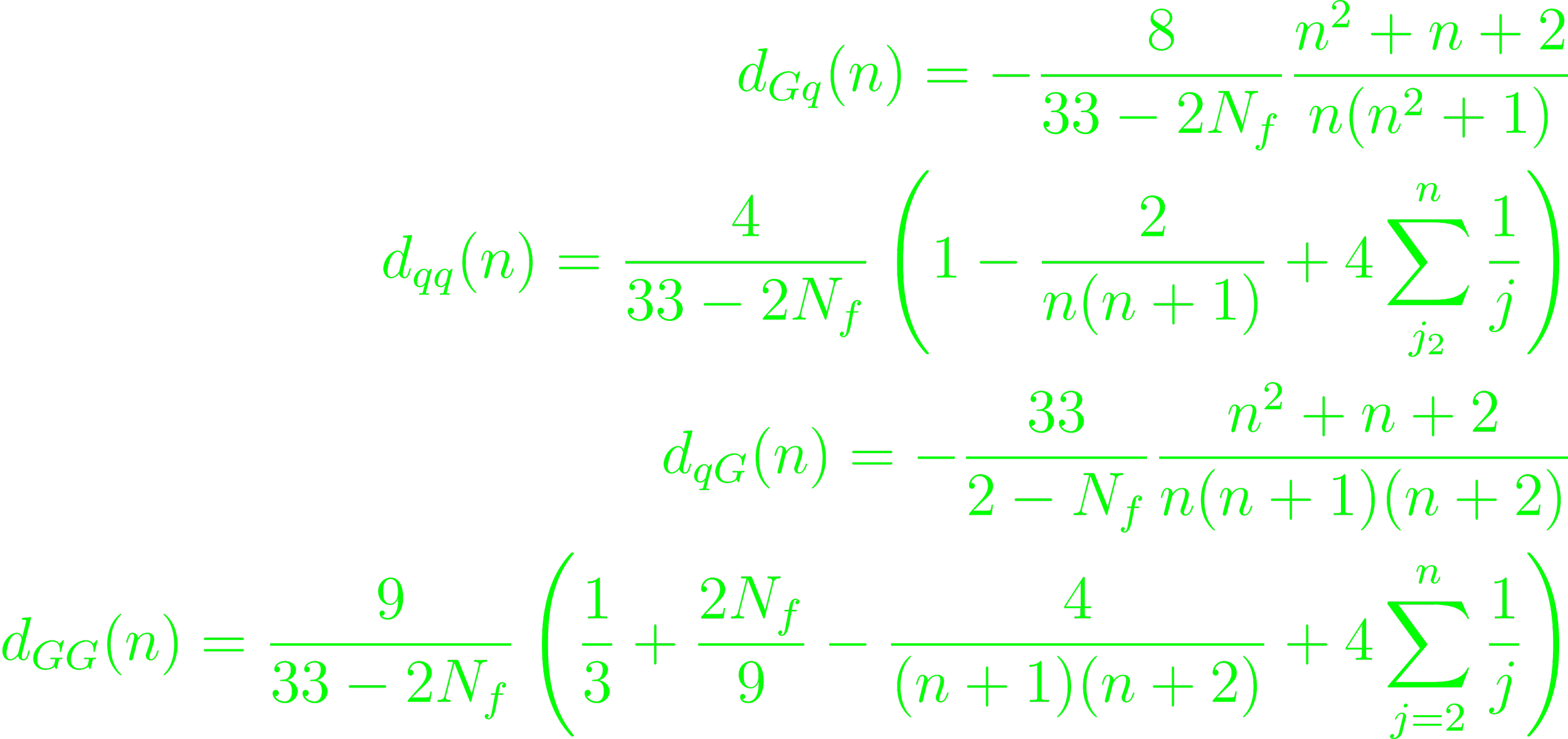Quantum Chromodynamics 2026, 06 - Alternative Approach to GLAP Equations & Distribution Functions
The GLAP equations can be derived alternatively purely through QCD properties. The fact that at large momentum transfers Q2, the hadronic structure becomes visible. The Q2 limit is related to the maximum transverse momentum of a parton in the final state. Note 1/√Q2 as the resolving power (p. 265). The GLAP equation is then derived through the distribution functions of partons involved in the interaction (Eq. 5.78).
Instead of the GLAP equations, the integral equations can be transformed directly into a set of linear equations, using the moments of the structure functions. An n-th moment is
(Eq. 5.84). Na is the structure function of the parton of kind a. Using the GLAP equations in this expression recovers the second integration over x' between x and 1 (Eq. 5.85 - 5.89), which in turn defines the splitting function by Pab(z),
(Eq. 5.90). The resulting system of linear functions are splitting functions:
(Eq. 5.91). The moments of the parton distributions M(n, Q2) are determined by experiment. At the renormalization point Q2 = μ2, the momentum transfer drops out. After the distribution for this point is known, the other ones can be determined easily through the GLAP equations (p. 283).