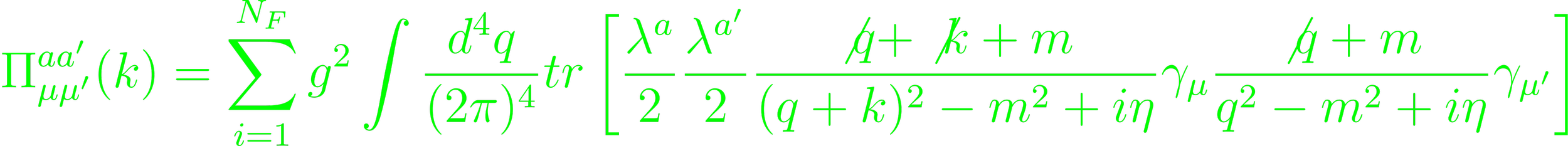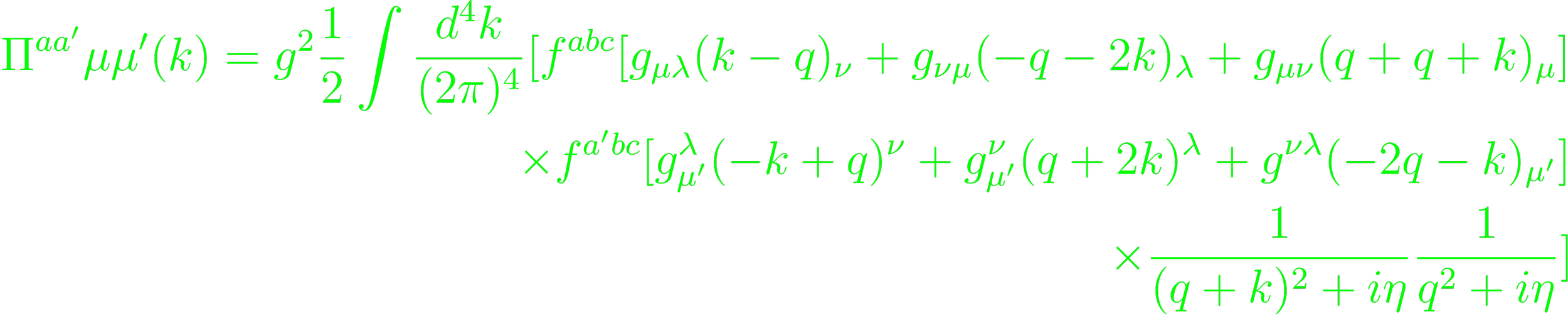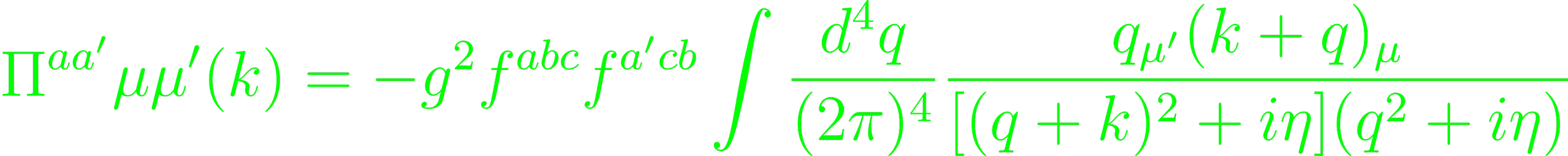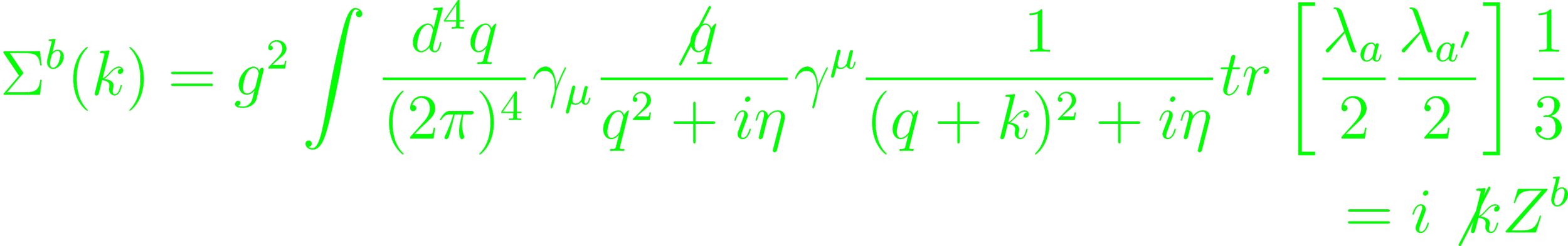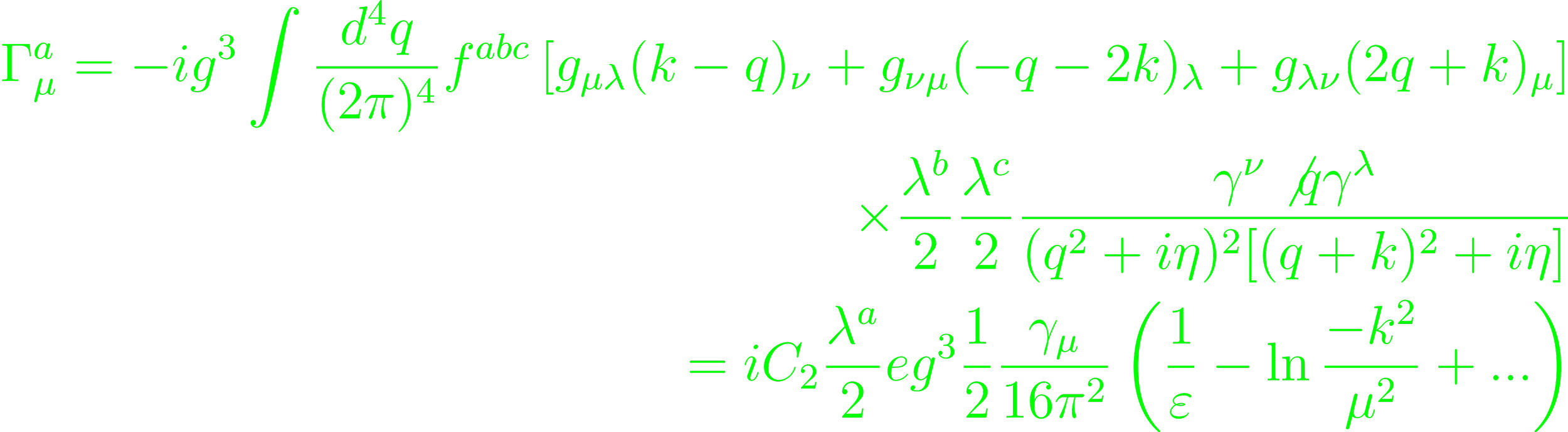Quantum Chromodynamics 2026, 04 - Renormalized Coupling Constant

Divergent Feynman diagrams can be renormalized. They fall into three classes. In the case of simple two-node loops, vacuum polarization applies (Fig. 4.14). Vacuum polarization graphs are proportional to the projector ensuring gauge invariance: (k_μk_μ' - g_μμ'k²)/k² (p. 203). The polarization tensor emerges from Feynman rules for QCD (Eq. 4.106):

In the denominator, q_μ → q'_μ = q_μ - k_μz (Eq. 4.109). By comparison of coefficient after contraction with the Lorentz tensor, include a factor of 1/4 (Eq. 4.111). Finally, the integral is exchanged (Eq. 4.113). The error function can be analyzed by setting d = 4 - 2ε (Eq. 4.114 - 4.121). In the case of a loop with two 3-gluon vertices,

(Eq. 1.122). The graphs that contribute are filtered through combinatorics (p. 209). The same follows for higher order contributions (p. 209 - 212). Separately, consider the ghost contribution

(Eq. 4.130). The shift from vacuum contribution reoccurs (Eq. 4.131) and the rest of the computation follows the schema of the vacuum contribution.

The self-energy graph follows a similar schema.

(p. 213, Eq. 4.134, 136). The vertex corrections are

(Eq. 4.137 - 4.138).