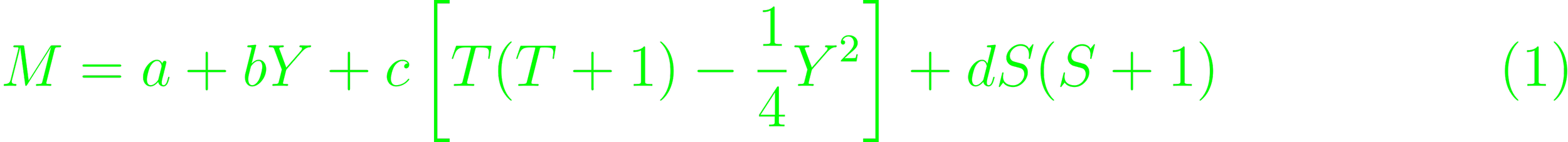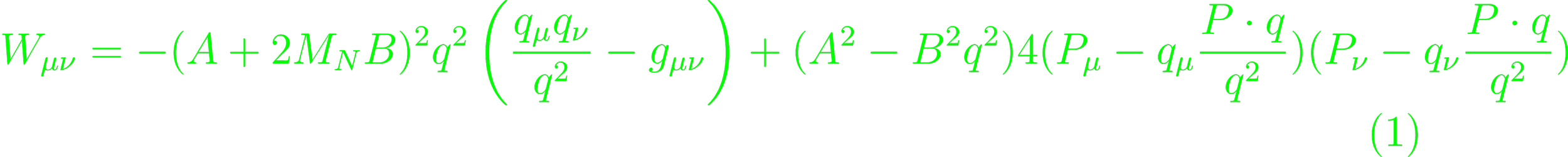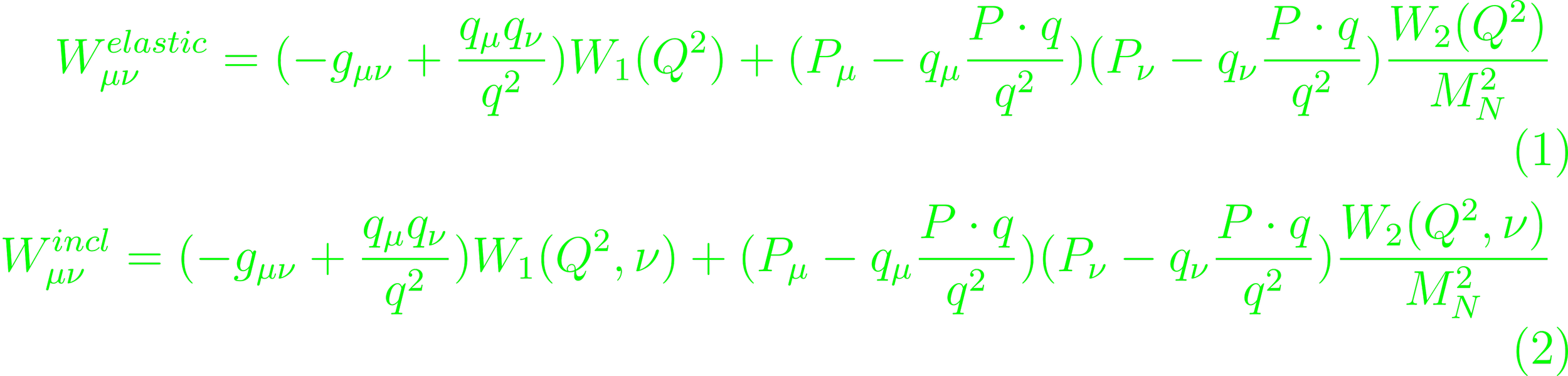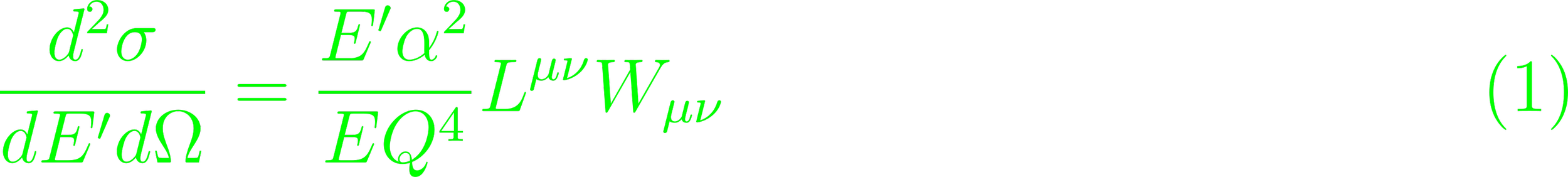Quantum Chromodynamics 2026, 02 - Scattering Reactions
Quark interactions don't immediately follow from the energies of the excitation states. The mass formula for mass differences in multiplet particles are derived from the symmetry-breaking in the flavour model applied to the quarks. The simplest one cited in the book as a product of the SU(6) flavour model is the Gursey-Radicati formula (Eq 3.1) that consists of the hypercharge, isospin and baryon spin.
The coefficients are used to fit the baryon resonances. For the six quark flavours, the flavour group SU(6) is used to model their symmetries. Since the quarks within the baryons can fill states with any angular momentum, the full dynamics are extended to include the full rotation group O(3), so the full symmetry group for the full baryon spectrum is SU(6) ⊗ O(3) (p. 77). This implies that every additional quark requires the extension of the SU(6) flavour group. Since some quarks are much heavier than the others, it's implied that the flavour symmetry is heavily broken.
The MIT bag model offers an alternative to the SU(6) flavour model. It posits that quarks can occupy all states that satisfy some boundary conditions, and that these exist for any angular momentum. This model needs heavy corrections. The Skyrmion bag model yields similar results (p.78).
Experimental data yields structure functions deduced from the scattering reactions (p. 80). To view the scattering as maximally pointlike, it needs to occur at high energies. It assumes that since high energy leptons travel at small wavelength, and as they don't have resolvable internal structure, the cross section of the reaction depends only on the baryon structure. Electron-nucleon scattering happens primarily through weak interaction, and should resolve the weak charge distribution. Given similar experiments can map the internal structure of the nucleon (p. 80). The most general structure of vertex function under electron-nucleon scattering is Γμ = Aγμ + BP'μ + CPμ + iDP'νσμν + iEPνσμν (Eq. 3.6). The Lorentz-invariant coefficients A, B, ..., E characterize the exact scattering. For this case, D = -E, C = B. The cross section is
(Eq. 3.15), and the elastic scattering tensor can be separated out, by defining new functions W1, W2 and Q2 = -q2. Similarly for the inclusive inelastic scattering tensor
(Eq. 3.16, 3.18). W1(Q2, ν), W2(Q2, ν) are structure functions for inclusive electron-nucleon scattering (p. 97). The differential cross section is the product of the full scattering tensors of both particles involved in the process. For electrons, that is Lμν = 2[pμp'ν + pνp'μ - gμν p p' + gμνm2]. For unpolarized electron-nucleon scattering in lab systems is
(Eq. 3.22).