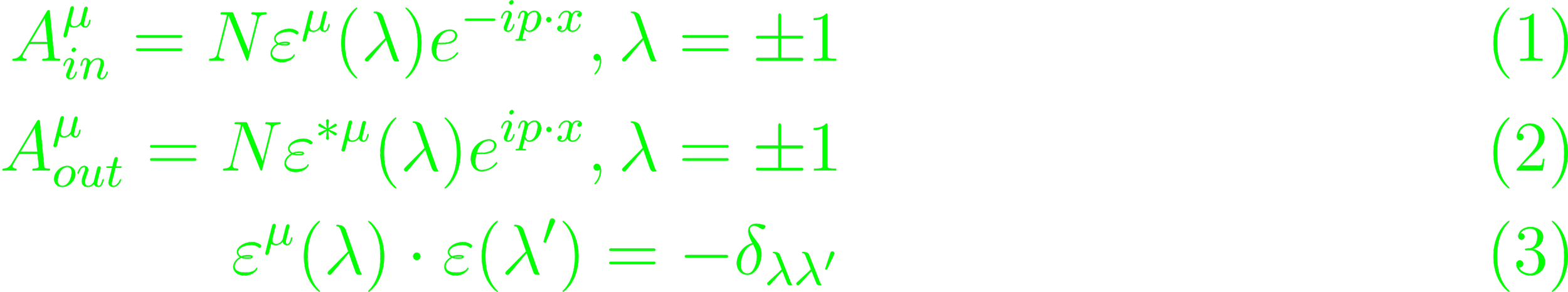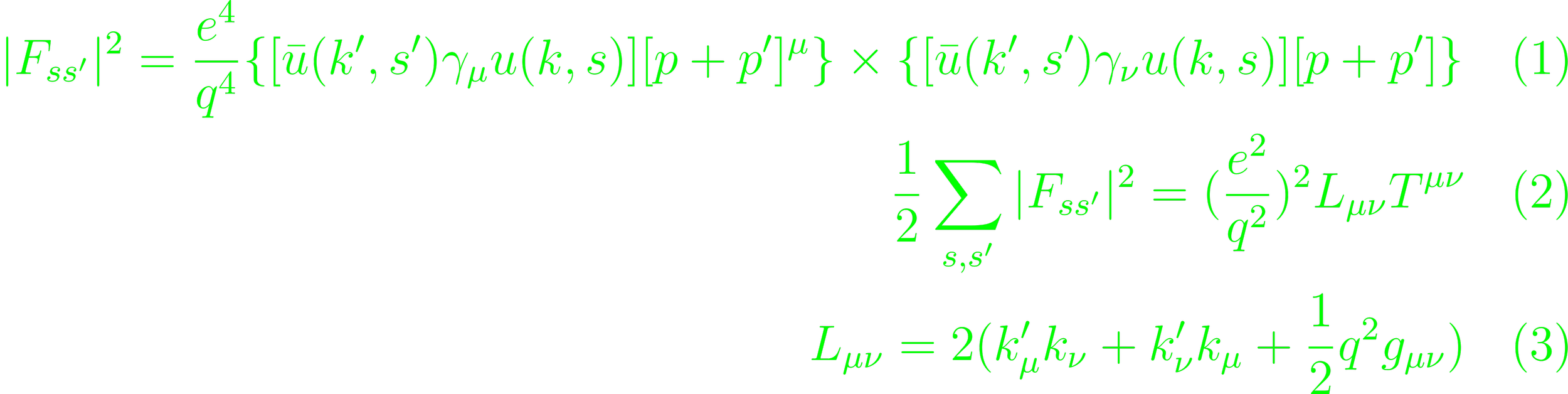Quantum Chromodynamics 2026, 01 - Polarization of Spin-1 Particles

For massive spin-1 bosons, apply the Proca theory, which emerge from the Lagrangian density of the classical 4-vector field ϕ^μ(x). The wave equation follows from it, and the definition of the field-strength tensor: ∂_αF^αμ + M²ϕ^μ = 0 (Eq. 2.121 - 122). By 4-divergence, M²∂_μϕ^μ vanishes (Eq. 2.123). Given a nonvanishing mass, the divergence has to vanish, which then supplies the Proca equation. The orthogonal polarization vectors for massive vector bosons can be written as cartensian unit vectors and in spherical representation using the parameter λ.

(Eq. 2.126a). Using this, write the wave equation as a superposition of linearly independent solutions ϕ^μ(x) = ∑_{λ=0, ±1} ε^μ(p; λ)e^{-ip x}, p² = M² (Eq. 2.130). The set of polarization vectors is complete.

Photons are massless spin-1 particles. Given a zero momentum is equivalent to a positive definite energy state, the momentum-vector must be nonzero at all times. This requires a different analysis. For free photon fields, the wave equation is ∂_μA^μ = 0 = □A^μ (Eq. 2.136). This, along with p² = 0, the solutions are plane waves (Eq. 2.137), which can be modified through a polarization vector. The field's symmetry is preserved in Lorentz gauge, given that the additional term satisfies the Klein-Gordon equation for the massless scalar field (Eq. 2.139 - 140). The full description of photons distinguish between incoming and outgoing photons with 4-momentum p and polarization λ

(Eq. 2.147 - 149).

The pion propagator emerges from the Green's function of its inhomogeneous Klein-Gordon equation. In momentum space, this Green's function is

(Eq. 2.153). The rest-mass and momentum are assumed unequal for virtual pions. Define the square scattering amplitude as part of the cross section F_ss' as

(Eq. 2.158, 161, 172)