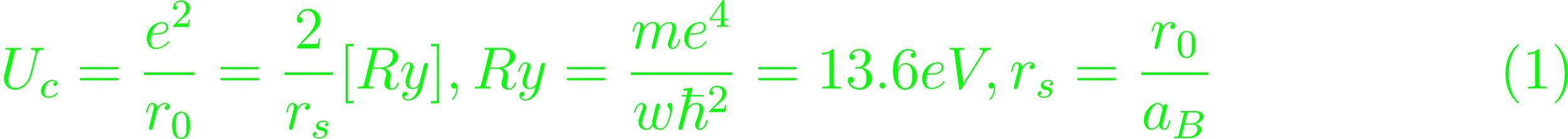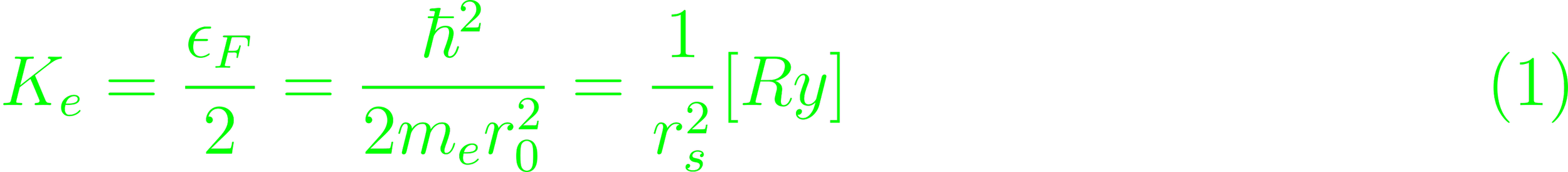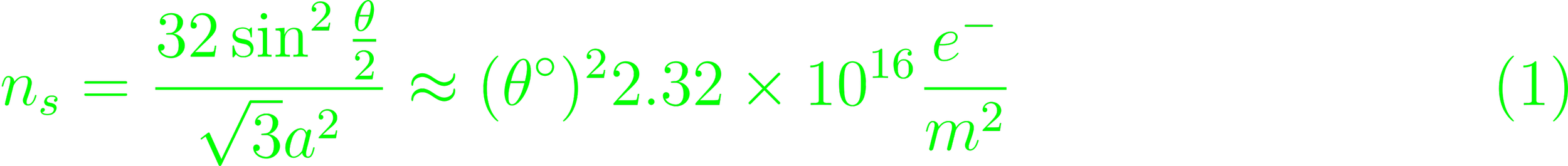January 2026 - Making Sure I'm Not Doing Wigner Crystal Research

When I found out about Coulomb crystals, I was initially somewhat worried, because the article I read hinted at Wigner Crystals being about the same concept, albeit using electrons, in which case what I was working on might have been redundant (up to a mass factor of 0.1), which would have been majorly demoralizing and likely a detriment for my own motivation to continue. As such, I approached the topic with some dread, but

At low temperatures and densities, electron motion slows down far enough for their electric charge to influence their interactions, causing them to crystallize into a quasi-solid. Strongly interacting electrons can break translation and orientation symmetry (i.e. the classical assumption that action of the particle is independent of its position in space and the direction its momentum vector is directed), leading them to crystallize spontaneously into a crystal structure, tuned to the electron density.

The first observation of such Wigner Crystals was made in bilayer graphene in a large perpendicular magnetic field at very low temperatures, imaged using scanning tunnelling microscopy (STM), probing the electron's wavefunction directly, and hence extracting data as to whether the crystallized lattice is ordered and how the lattice constant changes with particle density, and whether it melts into other quantum phases. The data is in line with predicted behavior for Wigner crystals. A zero-point motion for an electron has also been observed, occupying a significant amount (30%) of the lattice constant for its crystal site.

The theoretical condition for Wigner Crystals is that the external potential energy outcompetes the electron's kinetic energy at a crystallized inter-cell distance. The original conception featured an electron gas in a periodic potential. The Coulomb-interactions at low particle density, the electron-electron correlation energies diminish as r_s is increased. The particle energy on a lattice depends on the Coulomb potential and kinetic energy. The Coulomb interaction in ions increases quickly with increasing density, eclipsing the kinetic energy, and localizing the ions. For 2D systems of electrons with

the mean potential energy per electron is

The kinetic energy for a single electron in a simple electron spectrum is written

Relevant to the construction of Wigner Crystals is the r^-1 of the potential, and the r^-2 of the kinetic energy, which eventually suppresses the kinetic term for r_s >> 1. Electrons in ground state of such 2D systems were hence postulated to form a perfect lattice, an "electron solid". Wigner Crystals were long assumed to occur only under a non-zero external magnetic field, unless at densities low enough to make direct observation of the phenomenon very difficult. The required density could be elevated though, using layers of 2D lattices. In a study by Swierowsky two layers of Wigner lattices are brought to proximity while maintaining a large distance between the layers, so tunneling probability remains negligible. Coulomb interactions between the layers contributes to the potential. The group's numerical simulations hint at Wigner crystallization at about thrice the density than would usually be required. At inter-layer distances comparible to the lattice constant, the liquid phase would be restored to the crystal. In twisted bilayer graphene's superconducting rotation, the effects of moire supercells dominate, so that the inter-cell distance is defined by the lattice constant of the moire supercell. It sets the lattice constant a to

Physically, only the two lowest band of the crystal structure are important. They can house only 4 electrons due to Pauli's exclusion principle, and the supercell electron density evaluates to

far below the required density for Wigner crystallization.