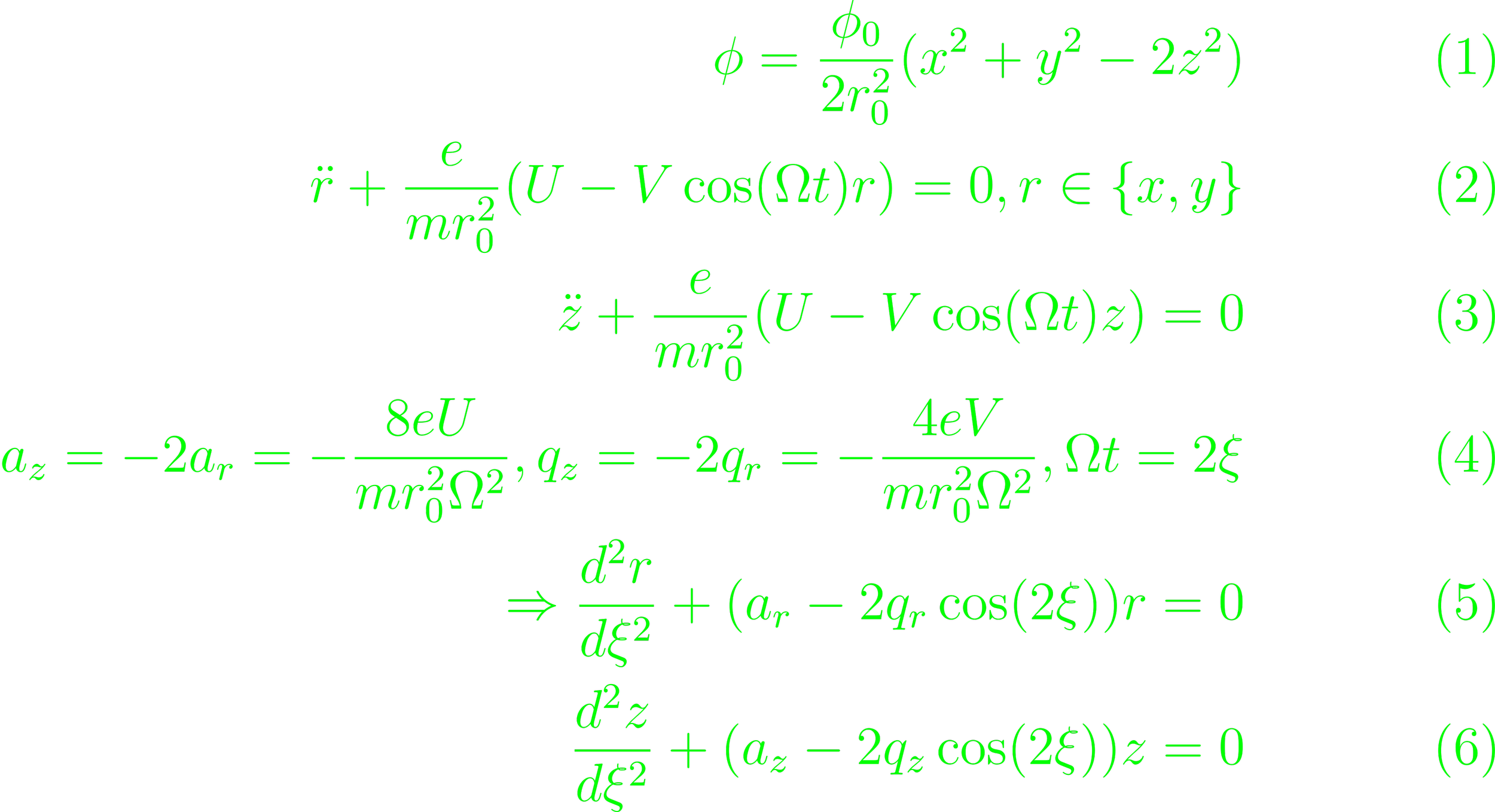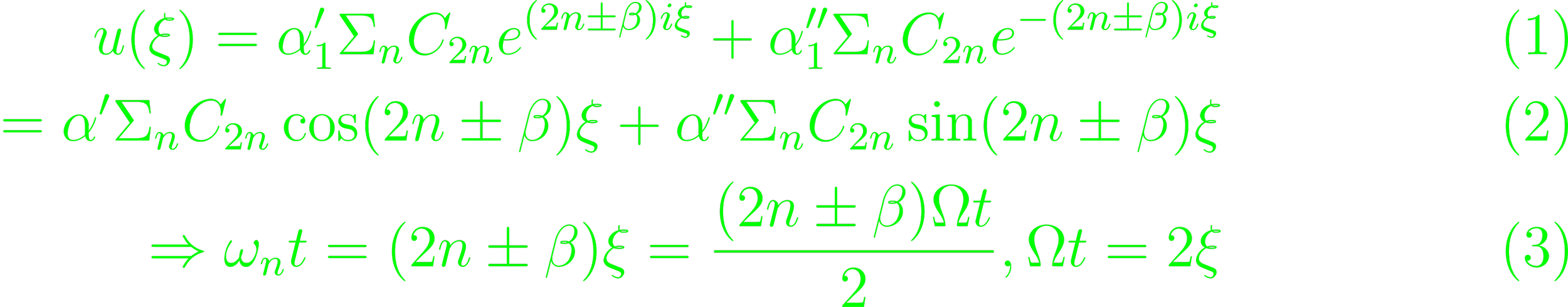December 2025 - Paul Traps
The alternative quadrupole trap construction to the Penning trap is the "Paul Trap". It tackles the problem posited by the Earnshaw Theorem head-on, by using oscillating electric fields, rather than static ones, and in exchange its construction aims to create hold a quadrupole charge in a (relatively) static position. The concept of the trap is rooted in the classical approach based in Gauss' law ∇ ˙ F =∇ ˙ (-∇ U) = -Δ U = 0, so the quadrupole potential will only be equipped with saddle-points, rather than actual minima. This presents an instability to be worked around, most easily by having it oscillate. This can be achieved by adding an oscillating voltage that has the potential alternate between two state, whose time-averaged potential has an effective minimum.
The typical Paul-Trap setup consists again of three electrodes, arranged in a line along the z-axis, and built rotationally symmetrical. The top and bottom electrodes are end-cap hyperbolic electrodes, the same distance away from the ring electrode oriented in the x-y plane between them.
Theoretically, a quadrupole potential produced by electric fields on the electrodes has the form $U(r) = Q\phi = Q\frac{\phi_0}{2r_0^2}(ax^2 + by^2 + cz^2)$ where ϕ is laplacian. r0 is the ring electrode radius, ϕ0 is an external potential and Q is the particle charge. A non-trivial constraint emerges a + b + c = 0. There is a 2D solution by setting c = 0 and a = -b, though this requires four rod electrodes with a hyperbolic surface turned inward, usable as a mass spectrometer. It's not so interesting for our purposes. A 3D solution requires that the hyperbolic end-cap electrodes are dimensioned so that r20 = 2z02 where z0 is the distance between the trap center end the end-cap electrodes. The constraint solutions are myriad, but a simple one would set $a = b, c = -(a+b)$. Setting a = 1, and
The results are the Mathieu equations, which have stable and unstable solutions. Interest is of course mainly on the stable solution