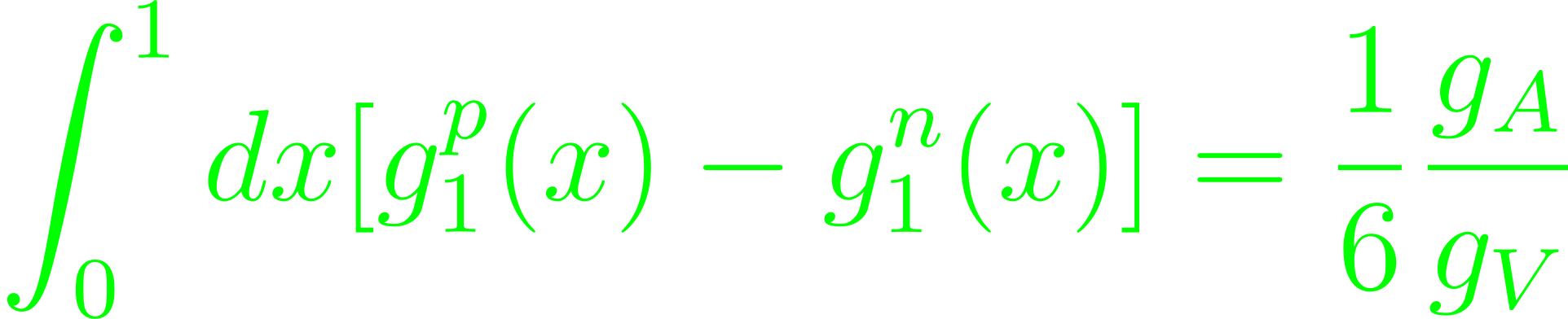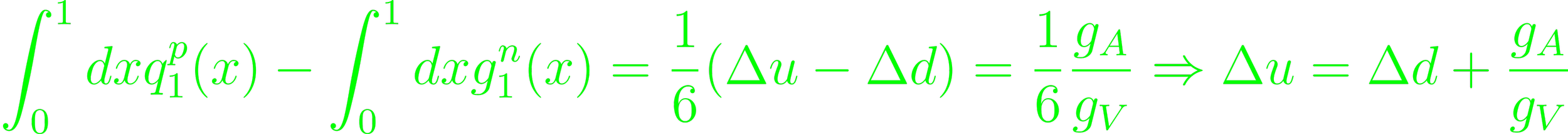Quantum Chromodynamics 2026, 08 - Wilson Coefficient

The OPE's separate scales allows for descriptions of moments of structure functions through coefficient functions. The matrix elements can be investigated with nonperturbative techniques. The key observation is that the coefficient function C_i(Q², μ²) is independent of the states emerging from the time-ordered product. Calculation of the Wilson coefficients are very long considerations going through the Feynman diagrams that belong to some time-ordered product. This process is very long, and a little hacky, utilizing otherwise obscure identities. (Section 5.5)

Spin-dependent structure functions play a role when scattered leptons and hadrons are polarized. With a polarized hadron, there is an additional Lorentz vector (spin vector). Retracing the analysis with its addition, Unpolarized structure functions can have the momentum fraction deduced from them. Given that these are carried by quarks, but only account for half of the total momentum, there needs to be something performing the gluon function. Polarized structure functions display how much of the proton spin is carried by quarks, how much by gluons and how much is due to angular momentum. In analyzing spin structure, there are several concepts (p. 360). The Bjorken and Ellis-Jaffe sum rule pulls the knowledge of axial vector coupling in weak interactions, into predictions based on isospin and SU(3) flavor symmetry for the integrals of g₁. The antisymmetric part of the hadronic scattering tensor can be written as an axial-vector forward matrix element of the proton. The proton couples to quarks and the asymmetric part of Δσ is proportional to a term using a well-known decomposition of the product of three gamma matrices (Eq. 5.299). The optical theorem yields an analogous cross-section, indicating zero momentum transfer. In combination,

(Eq. 5.304) that is the Bjorken-sum rule, connecting proton and neutron results. Higher-twist corrections are known, and expressed primarily through matrix elements, which can be calculated by QCD sum rule techniques. Along with the Ellis-Jaffe sum rule, it yields

which is an additional constraint for the matrix, joined by the coupling of s and u quarks in hyperon decays (p. 363).

The axial anomaly and the gluonic contribution to g₁(x) is important for hadronic physics by contributing to the spin structure function. For an isosinglet axial-vector current, this effect results in a split of fermion lines into a structure that implies that the constants c depend critically on the chosen infrared regulators, the OPE finds no gauge-independent local definition of ΔG, and gauge transformation with nonzero topological quantum number shifts contributions from Δq to ΔG (p. 365).