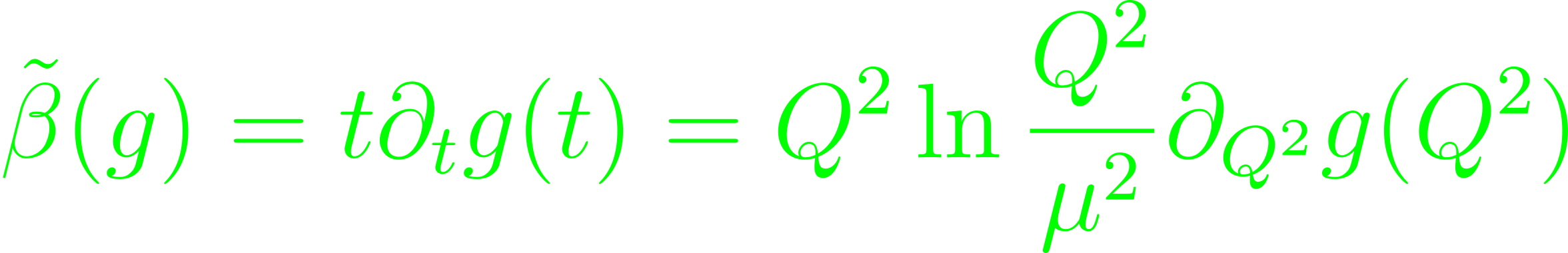Quantum Chromodynamics 2026, 07 - Renormalization and Expansion into Local Operators
There is a formalism to derive the GLAP equation in the operator product expansion (OPE). It's generally valid, and not subject to restrictions to the context of deep inelastic lepton nucleon scattering. The analysis starts with the definition for Wμμ', and applies it to the rest system of the nucleon. The physical final states are written in as a matrix element. After transforming the expression into the commutator form, the light cone expansion is applied (Eq. 5.121 - 5.131). Through properties of the γ-tensor, additional terms bring the expression into the typical form of the OPE (Eq. 5.133 - 5.135). The remaining divergent factors are the Wilson coefficients, which can be calculated through perturbation theory in terms as an expansion in the coupling constant αS (p. 295). In the Bjorken limit, short distances give the dominant contribution to the scattering tensor (p. 297). The expansion of Wμμ' changes if the free commutator is replaced by the exact current commutator. This corresponds in lowest order to the transition from the single parton model to the GLAP equation (p. 301).
The β-function emerges primarily from the coupling constant g, depending on the dimensionless quantity t, so that β = -∂tg(t), which, using the definition for the momentum transfer can be written as
(Eq. 5.184), which can be analyzed in its general case (p. 309). The zeros mark the behaviors at the large momentum transfers (ultraviolet limit) and the low-momentum transfers (infrared limit). At these, it can diverge, due to instability.
The factorization into a Q2-dependent perturbative part and fixed numbers A(n),j containing ∫01 dx xn-2F2(x, Q2) = 2πi∑j C(n)2,j (Q2, g, μ) A(n),j is fundamental to QCD applications (Eq. 5.214). It remains to show that this is still true in the presence of higher order terms. A soft gluon line couples strongly, so higher orders in QCD are in general as important as lowest order (p. 318).