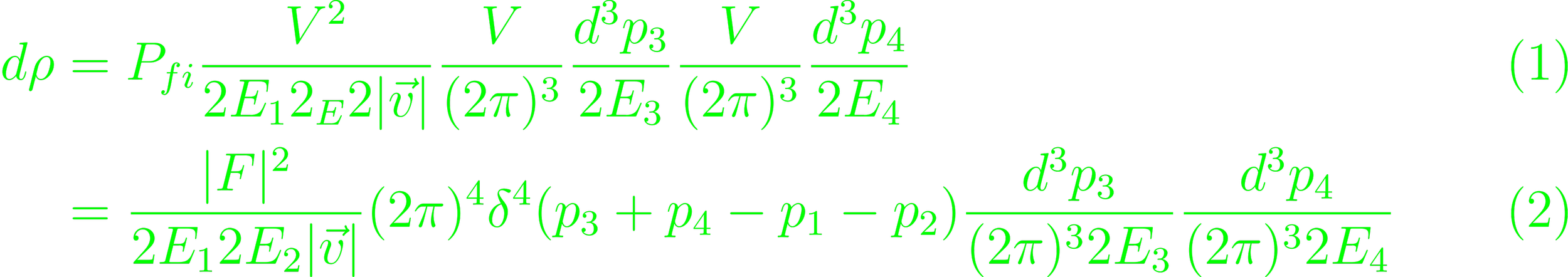Quantum Chromodynamics 2025, 52 - Pion QED
Scalar QED begins from the Klein-Gordon equation. (pμpμ - m02)ϕ(x, t) = 0 (Eq. 2.66). Plane waves that solve it can have either positive or negative energy, and adhere to the continuity equation. The probability current density is defined as j = 2|N|2p (Eq. 2.75), following the definition of the 4-current density and the probability density, which, due to the full spectrum of energy, can be negative. This is described by the Feynman-Stueckelberg prescription that negative energy solutions have a particle propagating backward in time, and a positive energy solution have an antiparticle propagating forward in time (p. 27). The Klein-Gordon equation applies for neutral and charged mesons. A charged Klein-Gordon field for charged pions have a charged density current of
(Eq. 2.77-78). For its interaction with a generalized potential Aμ sets the solution of the Klein-Gordon equation to -Vϕ, where the potential reduces to V(x) = ie(∂μAμ(x) + Aμ(x)∂μ). The scattering in the S-matrix is S(1)fi = -i∫d4xϕ*fVϕi, which by inserting the definition of the plane waves evaluates to -ieNiNf(pi + pf)μAμ(q) and 4-momentum transfer q = pi - pf.
The S-matrix element of a Pion-Kaon derives from the spins of the particles. Positive kaons are spin-0 mesons, and it obeys the same wave equation as the pion. They don't obey the Pauli-exclusion principle, and the remaining effects stem from the electric charge (2.2.3, p. 32). Assume both are positively charged. The Maxwell equations reduce to □Aμ = jμem (Eq. 2.95). Define the inverse d'Alembertian that shows up in the definition of Aμ by its action. The cross section of plane waves for some probability density ρi = |Ni|22Ei (Eq. 2.106). ρ and E are zero-components of the 4-vectors (2.2.4, p 35). The full cross-section is written as
(Eq 2.116). The Lorentz-invariant phase-space factor (Lips) is defined so that the cross-section can be written using the Mandelstam variable s = (p1 + p2)2. Using the Lorentz-invariant flux factor,
(Eq. 2.117, 119, 120).