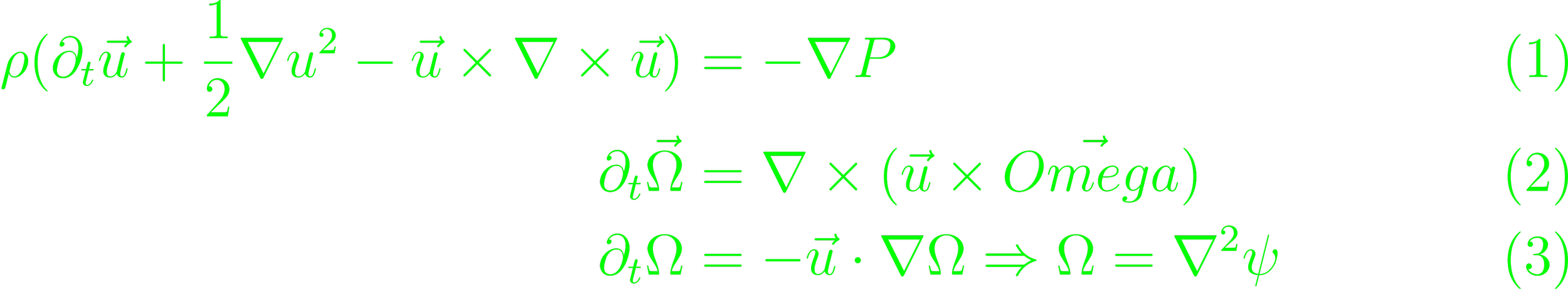Fundamentals of Plasma Physics 2025, 47 - Brillouin Flow
The chapter on Brillouin Flow uses cylindrical coordinate system {r, θ, z}, and initially considers forces on infinitely long cylindrical clouds of cold charged particles with the same polarity. It's not at radial equilibrium and expands infinitely along the r-axis. The cloud optionally rotates. When it does, an external axial magnetic field induces a force pushing the charged particles radially inwards, countering Coulomb repulsion and centrifugal force. For one-component plasma, no frictional drag due to collisions with opposite charge polarity is considered. Since the plasma is cold, the pressure is 0. The plasma is then described by the state equations.
Fast motions of plasma constituents in the axial direction smears out the axial structure, so that the plasma is effectively axially uniform at first approximations in time-dependencies. The particle drift is derived from the continuity equation and Poisson equation.
For an incompressible plasma (ρ(r, t) = const.), the continuity equation reduce to ∇u = 0. The vorticity vector Ω = ∇ × u has the form of the MHD induction equation.
In non-neutral plasmas, collisions don't degrade confinement, if axisymmetry is maintained. This is enables near perfect confinement in plasma traps. This is due to the conservation of total angular momentum of colliding particles, because all collisions of equally charged particles are elastic ones. Radial transport requires momentum exchange, which doesn't occur when the constituents are only of a single type.
Linear waves of non-neutral plasmas are written through Poisson's equation, and using cylindrical geometry, the l-th azimuthal mode with time-dependence e-iωlt, so that the equilibrium azimuthal velocity works out to
Via transformations,
This describes the non-axisymmetric diocotron modes of the plasma. These modes are affected from the otherwise neglectable wall boundary condition. For l = 1, the diocotron mode is exactly solvable. The linearized current density of the diocotron modes are written as J1 = n1qu0 + n0qu1. Their energy, via definition,
The middle line of the energy differential is the defined only by the axial length L and the wall boundary coordinate a. The 1-mode is a negative energy mode.
Assuming the wall has an insulated segment of length Ls and angular extent Δ, connected to ground via a small resistor R. The wall is near ground potential, and there are no electric fields exterior to the wall or just outside it. The diocotron mode works out to