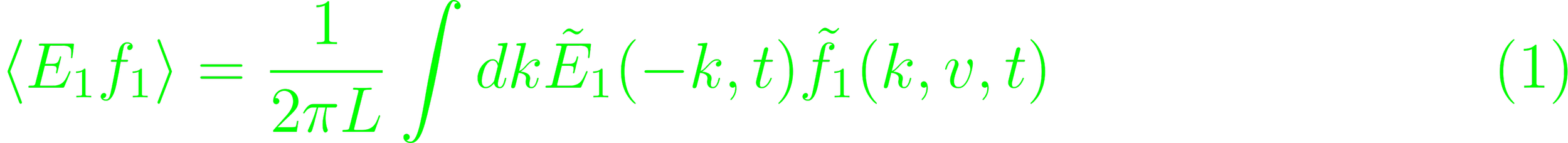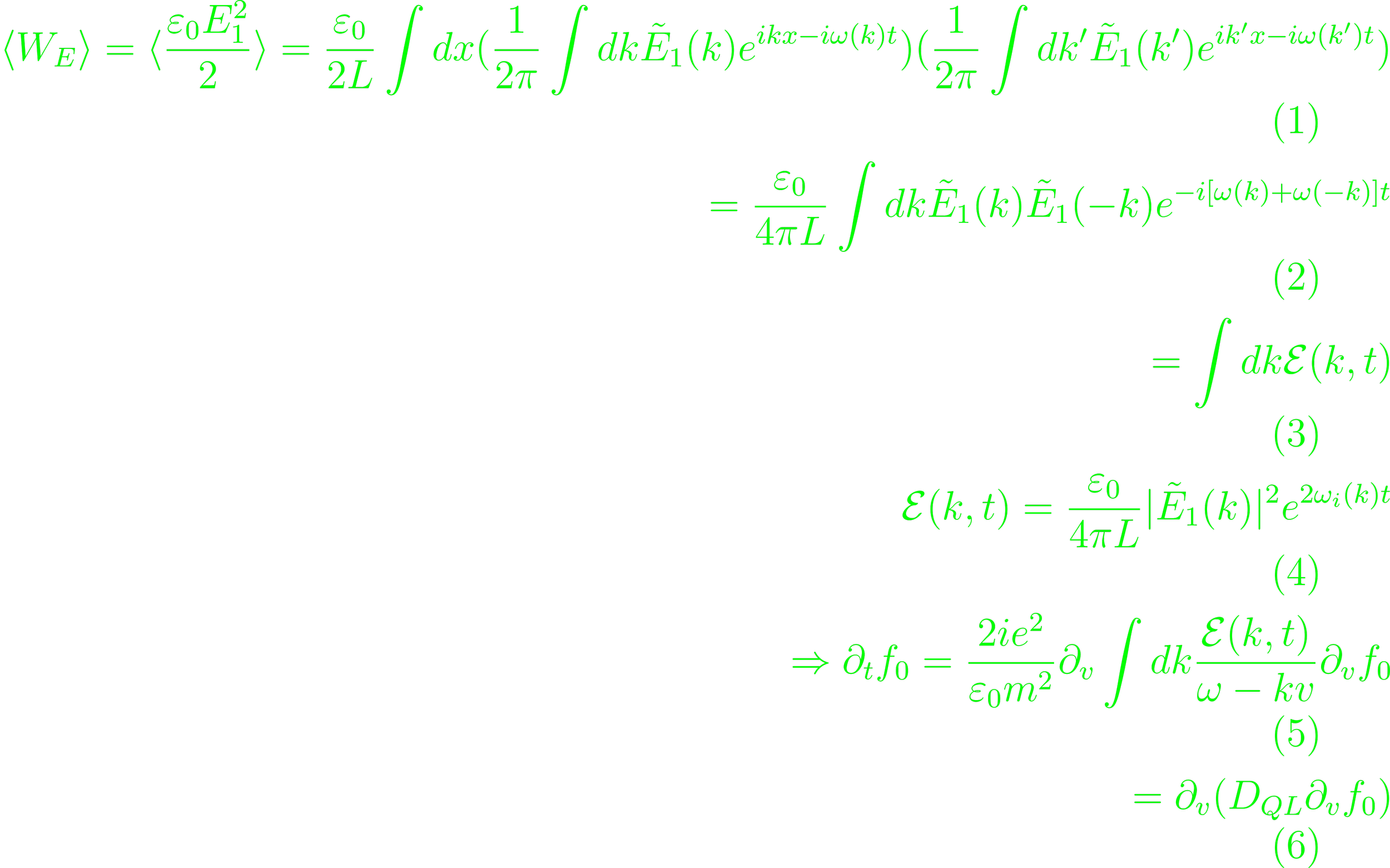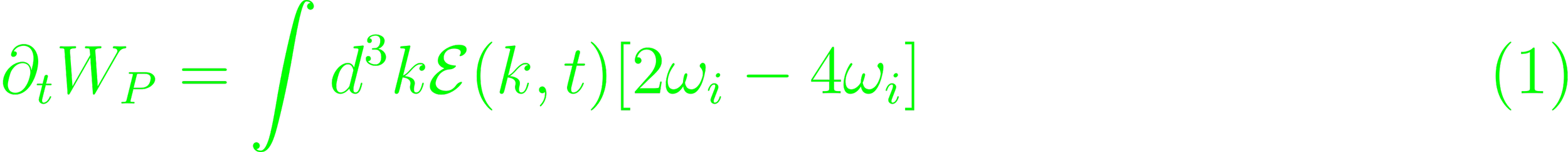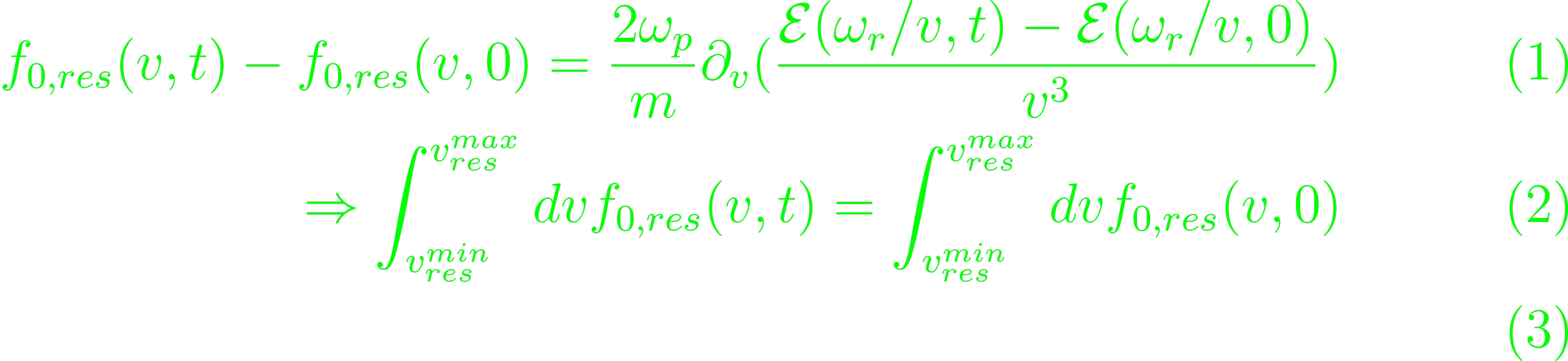Fundamentals of Plasma Physics 2025, 42 - Wave-Particle Nonlinearity
Assume a one-dimensional, uniform, unmagnetized plasma, considering only electrostatic modes and neglecting ion motion. It's characterized by coupled Vlasov and Poisson equations for electrons, and ion contribution is only a static, uniform neutralizing background. The electron velocity distribution function can be decomposed into a spatially independent equilibrium term with optional slow temporal variations, and a small high frequency perturbation with space-time dependence associated with spectra of linear plasma waves. The electron velocity distribution f and electric field E is a sum of indexed contributions. By assumption, f0(v, t) is independent of position, so define a velocity-normalized order zero distribution function whose integral is unity, using a scale-factor n0. This results in a quasi-linear velocity-space diffusion equation ∂tf0 = e/m ∂v⟨E1f1⟩ with
The volume average of the electric field energy
Particle conservation occurs automatically, as the zero-th moment of the velocity-space diffusion's derivative vanishes. The conservation of momentum emerges from the definition of the collective momentum ∂tnmu = -m∫v DQL∂vf0, which vanishes using the linear dispersion relation. Energy is conserved similarly.
For resonant particles, kv ≈ ω, which leads to extensive approximation in the time-derivative of the particle energy.
Further expansion yields an imaginary component which must vanish. The time-derivative of the particle energy can be split into a resonant and non-resonant component. This sum expresses in a 2ωi term of the non-resonant contribution and a 4ωi term of the resonant contribution. The resonant kinetic energy is equal to the non-resonant kinetic energy, and the energy in the electric field, so the latter two, which make up the wave energy, are equal.
For resonant particles, their total energy is not conserved, and can't be exchanged with wave energy. The 0-th moment is conserved, the second isn't. However, the total particle number is conserved.
The non-resonant particles experience a general reduction in kinetic energy, as well as a reduction in the electric field energy. This energy is transferred to the resonant particles.