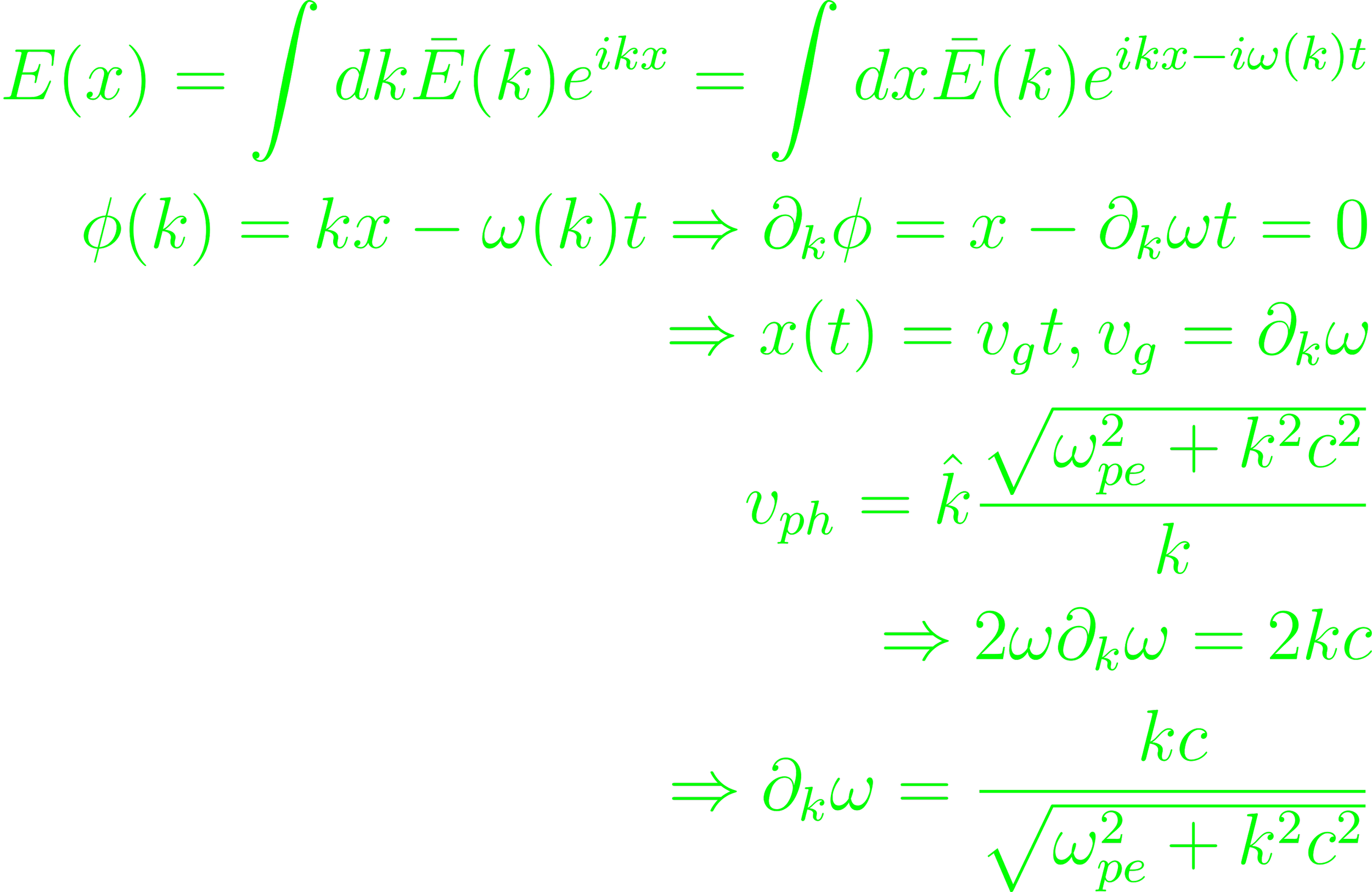Fundamentals of Plasma Physics 2025, 28 - Group Velocity

The electric field of some mode can be decomposed into spatial Fourier modes, varying over e^ikx. Later, consideration of the "phase mix" may factor in phase mixing and destructive interference. This defines the group, and later phase velocities.

Waves can either be electrostatic (∇×E = 0, E = -∇ϕ) or inductive (∇E = 0, E = -∂_tA). For Fourier modes, replace ∇ with ik, so then k and E is parallel for electrostatic modes, and such waves are longitudinal. EM waves have kE = 0, and thus are transverse. When the roots of the dispersion An⁴ - Bn² + C = 0 are well separated, the slow mode assumed at n² large. Either A vanishes, or B is infinite. At A → 0 , the dispersion relation is dependent on θ, and v_g in this situation can be evaluated by k²_xS + k²_zP = 0. It follows that k∂_kω = 0, so the group velocity and phase velocity are orthogonal.