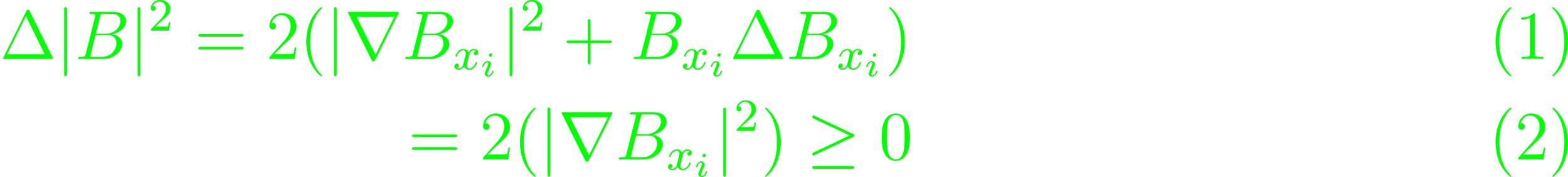October 2025 - Earnshaw's Theorem
Earnshaw's Theorem is one that is somewhat easily stated, but not entirely intuitive in its derivation. It states that a collection of point charges can't be maintained in stable stationary equilibrium configurations by the particle-particle interactions themselves. It was devised first for electrostatics, but it functions in the same way for magnetism, and gravitational forces. For soft magnets, the theorem requires a slight extension.
This is not a contradiction to the existence of solid matter and crystal structures, as the charges in matter are not isolated point charges, but rather distributed in matter. Other systems of isolated bodies usually feature accelerations, but this was disallowed by models of the atom that saw the electrons as isolated particles. The solution was provided by the QM approach of expressing electrons as charge densities in some volume within the particles, separated in energy state by the Pauli exclusion principle.
Underlying the proofs for different situations is that the Laplacian of each magnetic field component is also zero, which is mostly shown by invoking magnetic field properties anchored in the Maxwell equations of electrodynamics, namely that both the curl of and the divergence of magnetic fields vanish.
For fixed-orientation magnetic dipoles, the Earnshaw Theorem is written as ΔU = 0. Write the energy U of the magnetic dipole M as U = -M ˙ B, which is linear in the Laplacian, and can be rearranged
If the magnetic dipole is aligned with external field lines, one needs to show that U = -k|B|2. Using the same statement to be proved, the constant k can be divided out, leaving to argue that Δ|B|2 = 0. Using the aforementioned statement that ΔBxi = 0,
In paramagnetic materials, this indicates that its Laplacian of the energy is never positive, and there can't be any stable levitation, and in diamagnetic materials, the Laplacian of the energy can't be negative, so a potential can't have points with instabilities in all directions.