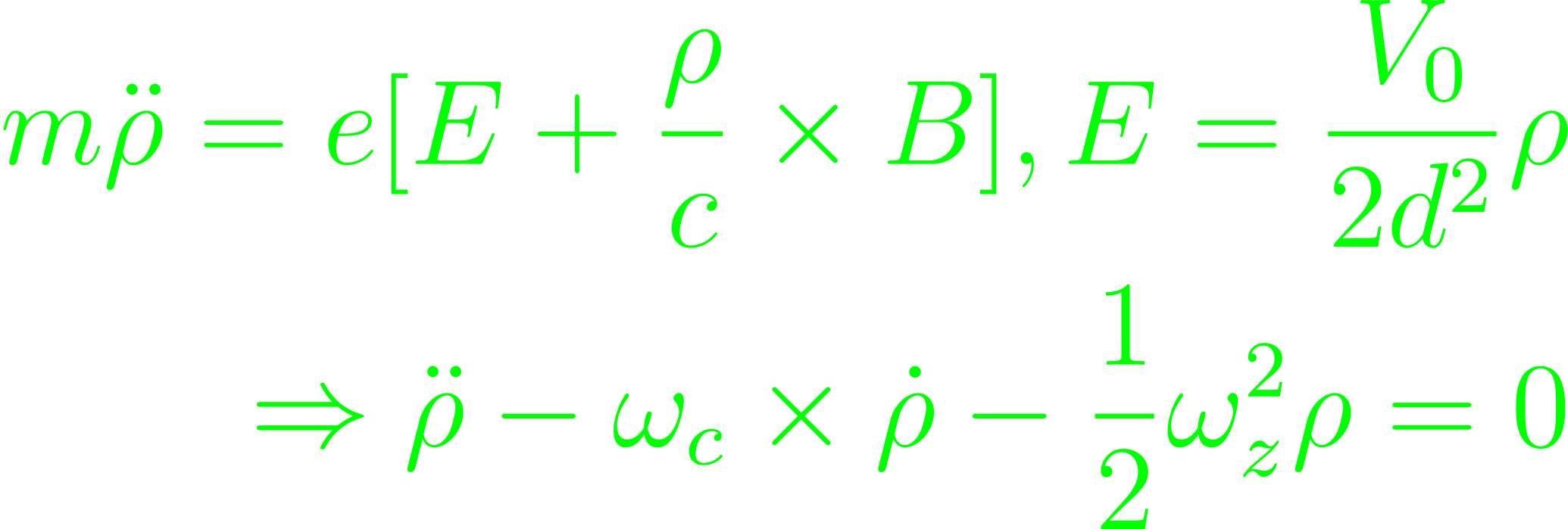July 2025 - Penning Traps

The Penning Trap is meant to utilize a target's quadrupole field (primarily) to trap it in the way traditional ion traps would hold them. The particles are meant to be held indefinitely in a combined homogenous B-field along with the Penning trap, itself an electrostatic quadrupole field. The beam of the electrons collides with sparse neutral particles, producing slow electrons, eventually captured. The quadrupole electrodes are hypoboloids, inducing spiral fields, acting ultimately like a quadrupole field. In full superposition, the particle motion are small radius cyclotronic motions, along with a slow circular magnetron drift motion in large orbits, i.e., tight curves along a torus. Note charge e, mass m, and assume B along the z-axis. This notes ω_c = |eB|/(mc). In an ideal Penning trap, a restoring force is superimposed by a quadrupole field, to offset small perturbations. A Laplacian potential for this purpose is V = V₀(z²-ρ²/2)/(2d²), which can be produced by two end-cap electrodes, and one ring electrode along equipotential contours. The Axial motion is decoupled from the B-field, leading to a simple harmonic motion. For the radial motion,

The Magnetron motion stems from the typical Lorentz Force, introducing the classical drift to a charged particle: u = cE×B/B². The terms are canceled in the basic case, but we can substitute for E. So much for the basic motions. The interesting additions are found in the nuclear physics' radiation damping stemming from charge acceleration. As the motion is cyclotronic, these terms can't be neglected. The energy in a cyclotron orbit is characterized as E(t) = E₀e^γ_ct, which when written in terms in radius:

The momentum p by a standard Lagrangian,